Описание

Постановка задачи

Предположим, вы заказали некоторый товар в интернете и хотите, чтобы его привезли прямо вам в руки. Или решили сами порадовать кого-нибудь посылкой — и чтобы адресату не пришлось для её получения покидать пределы квартиры. В обоих случаях вас, конечно, интересует, когда будет доставлена посылка; причём желательно, чтобы это время определялось точнее, чем «где-то в течение двух-трёх часов». И вы не одиноки в своём желании: компаниям, клиенты которых ожидают прибытия посылки, тоже важно знать максимально детальное время доставки.

В последнее время задачи прогнозирования времени доставки стали часто встречаться на различных соревновательных платформах вроде Kaggle, где их ставят компании от гигантов типа DHL до совсем небольших стартапов. Любой человек может принять участие в конкурсе и попытаться решить задачу: достаточно располагать данными о предыдущих доставках (которые предоставляет сама компания) и выбрать один из алгоритмов машинного обучения, будь то классический XGBoost, или его конкурент LightGBM, или что-либо другое на ваш вкус. Подкрутив параметры и насобирав фич, вы получите решение, которое наверняка окажется в десятке лидеров – при этом вам даже не обязательно разбираться в том, что именно происходит внутри алгоритма.

Пойдём дальше и представим, что именно ваше решение выиграло конкурс и компания-организатор внедряет его в работу. Теперь, заказав доставку, вы получаете сообщение наподобие «Ваш товар прибудет через 45 минут». Но что делать, если прошёл уже час, а курьера всё нет? Стоит подождать ещё чуть-чуть или пора составлять жалобу в отдел поддержки клиентов? Вот если бы вы могли знать не просто наиболее вероятное время доставки, а некоторый временной интервал, в течение которого доставка произойдёт с вероятностью 95, 90 или 85 процентов! Увы, ваше решение выдаёт лишь одно конкретное значение.

Процесс решения задачи

Чтобы найти распределение времени доставки посылки, нам в первую очередь нужно составить маршрут, по которому эта доставка осуществляется. Координаты пунктов приёма и вручения посылки, предоставленные Sendy, определяют начало и конец пути. С помощью пакета OSMnx мы получаем разбиение этого пути на участки и их длины, а база данных Uber предоставляет почасовое значение средних скоростей на каждом участке.

Нашу задачу составления маршрута делает осуществимой то, что дороги в OSMnx и Uber разбиваются по одинаковой схеме: крупным элементам (это могут быть прямая проезжая часть, перекрёсток, кольцо) присваивается уникальный номер и, дополнительно, каждый участок разбиения кодируется номерами своих начальной и конечной точек (узлов). Однако зачастую возникают проблемы, связанные с пропуском данных в одном из источников: например, какие-то узлы из OSMnx отсутствуют в Uber или наоборот. Разобравшись с этими трудностями, мы смогли составить рабочий алгоритм построения пути между точками A и B, который затем был с успехом апробирован на 100 наиболее популярных маршрутах из данных Sendy.

Типичными распределениями скоростей для однородного участка дороги, используемыми в литературе, являются нормальные, логнормальные, гамма-распределения, распределения вейбулловского типа и их композиции. На графиках 1 приведены гистограммы скоростей из Uber в вечернее время на участках с номерами 16 и 17 некоторого маршрута.

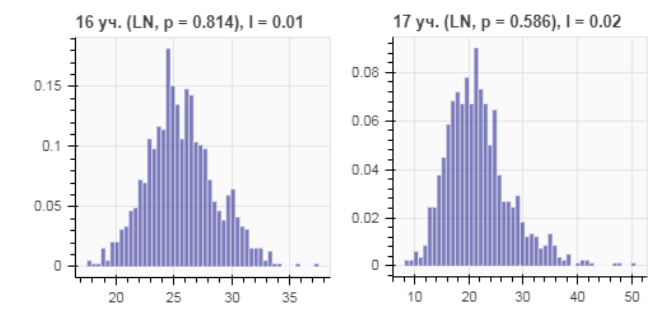
Рис. 1: Гистограммы почасовых значений скоростей (км/ч) из базы данных Uber в вечернее время (16:00 – 19:59) на некоторых участках дороги. Длины участков равны 11 и 23 метрам соответственно, а скорости варьируются от 5 до 55 км/ч. Указаны p-значения по критерию Колмогорова-Смирнова для логнормального распределения с оценками максимального правдоподобия.

На основе наших исследований, мы предполагаем, что скорости на участках имеют или нормальное распределение, или логнормальное, или их бимодальные и тримодальные аналоги. Выбор на каждом участке дороги проводился на основе критерия Колмогорова-Смирнова. Критерий выдаёт p-значение, принимающее значения от нуля до единицы, и чем оно больше, тем «увереннее» мы в выбранном распределении.

Для проверки этой гипотезы мы масштабируем выборку: если изначальная выборка соответствует логнормальному распределению, то после взятия логарифма выборка должна иметь нормальное распределение. При выполнении предположения нормальности, после соответствующих сдвигов, поворотов и растяжений координаты выборки должны стать независимыми, а сама выборка должна образовывать один кластер. На рисунке 2 изображены скорости на тех же участках до и после трансформации

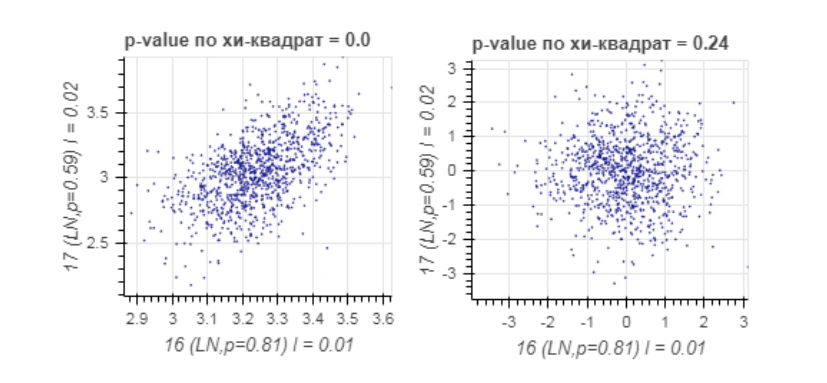
Рис. 2: Диаграммы рассеяния трансформированных скоростей на выбранных двух участках дороги. Слева скорости на обоих участках были прологарифмированы. Справа к получившемся значениям мы применили сдвиг и поворот, используя эмпирические средние и ковариационную матрицу. Указаны p-значения по критерию хи-квадрат для независимости компонент вектора.

С помощью критерия хи-квадрат мы проверяем попарную независимость выборок и тем самым оцениваем наше предположение о нормальности масштабированных данных. Легко заметить, что на левом графике скорости на 16 и 17 участках зависимы и p-значение равно 0, в то время как на правом они независимы и p-значение уже существенно больше нуля.

Преимущество вероятностного решения

Решая задачу таким образом, в ответе мы получаем распределение времени доставки. Оно представляет собой функцию, которая говорит нам о том, с какой уверенностью мы можем утверждать, что посылку доставят за то или иное время. Это зачастую гораздо интереснее, чем знать только один, наиболее правдоподобный исход (хотя обычно ответ на подобные задачи звучит именно так: лишь одно, в лучшем случае наиболее вероятное, значение — вот за такое время доставят посылку, и только!).

Знание распределения позволяет давать ответы на разные интересные вопросы. Например, «стоит ли ждать, что курьер справится быстрее, чем за полчаса?». Или «в каких временных границах (от и до) будет доставлена посылка с очень большой вероятностью, скажем, 90%?». Эти границы еще называются доверительными интервалами (ДИ).

С помощью доверительных интервалов можно «ловить» аномальные заказы, вроде тех, когда курьер не слишком торопился с доставкой и потратил значительно больше времени, чем мы предсказывали. Или наоборот, решил обмануть программу и указать время доставки намного раньше. На рисунке 3 вы видите результат нашей работы по одному из маршрутов доставки. Можно заметить, что, к примеру, на графике 3a, три заказа, лежащих правее правой границы ДИ, доставлялись слишком медленно, а пять левее левой – слишком быстро.

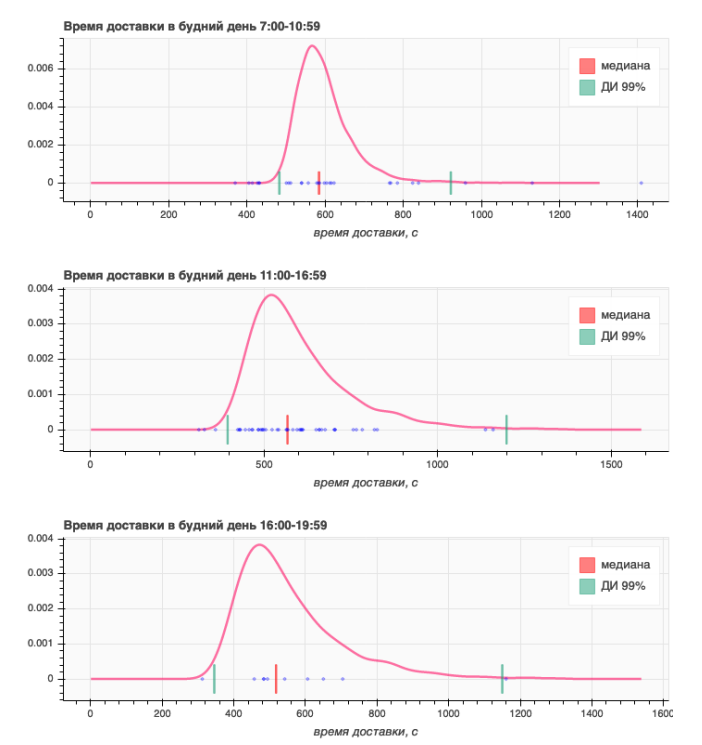
Рис. 3: Сравнение предсказания с реальными данными. Розовая линия — полученная нами плотность времени доставки. Красная вертикальная линия – медиана, посчитанная по этой плотности. Две вертикальные зеленые линии — границы 99%-го доверительного интервала: внутри этих границ время доставки заказа, исходя из нашей модели, будет сосредоточено с вероятностью 99%. Синими точками обозначены реальные заказы из базы данных Sendy.

Анализируя построенную модель, мы можем делать выводы о том, каким образом различные факторы (вроде дня недели и времени суток, когда была осуществлена доставка, и т.д.) влияют на время доставки, и, соответственно, давать максимально корректный его прогноз. Эта информация подскажет логистической компании, на что следует обратить внимание, чтобы улучшить сервис.

Итоги проекта

Наша команда смогла получить решение, которое по произвольным координатам приема и доставки посылок и по времени, когда курьер принимает заказ, строит распределение времени доставки, а также его графическое представление, но на этом проект в рамках Большой математической мастерской завершился.